Braess Paradox

Braess paradox refers to the finding that total network efficiency in the user equilibrium may recline if the network is equipped with extra capacity, i.e., a road is added to the network. Consider the following network, also referred to as Braess Network.

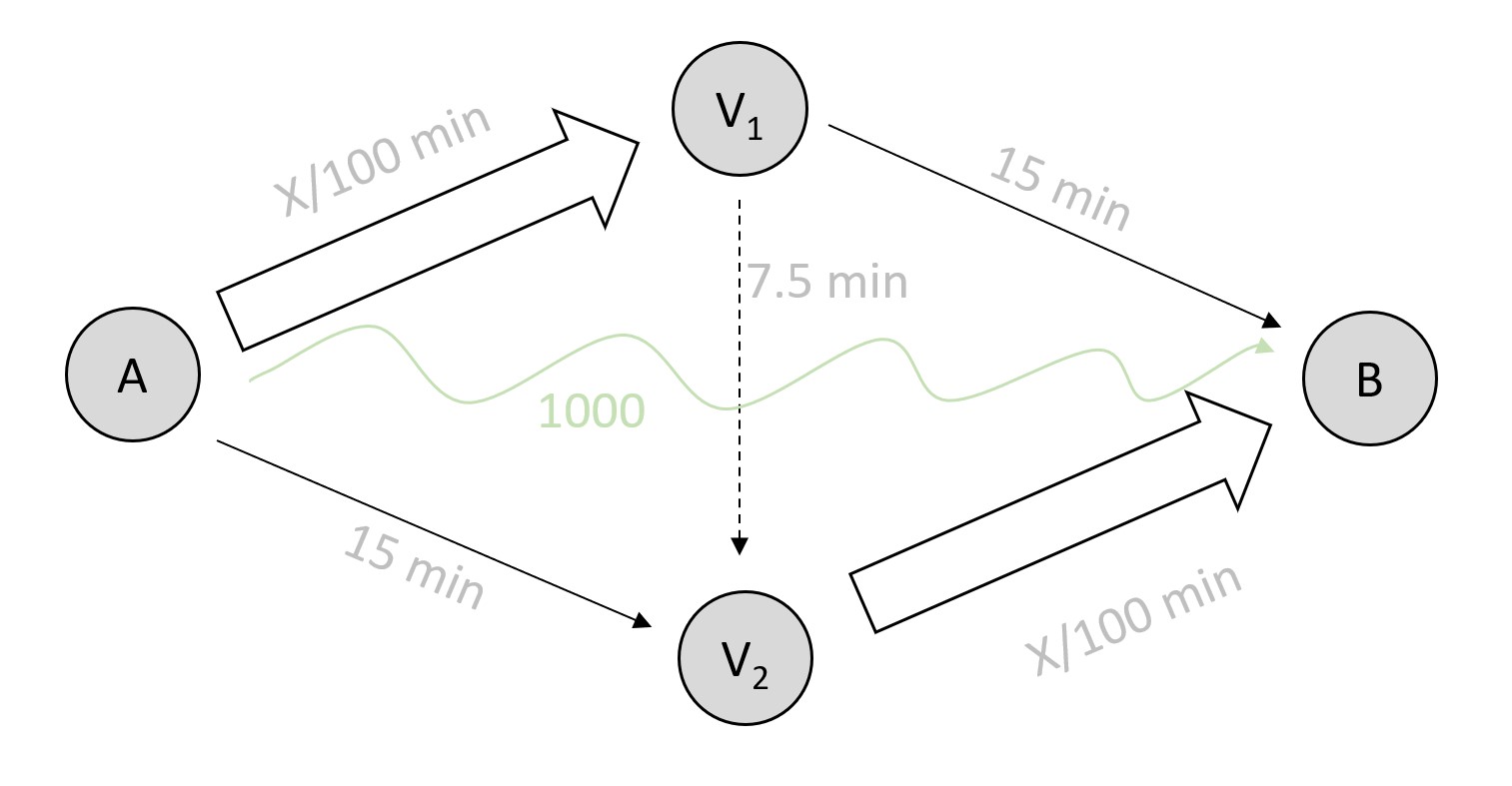
Braess paradox.

Network specifications

Drivers wish to travel from vertex \(A\) to vertex \(B\), and in the default case (i.e., without the articial edge connecting \(V_1\) and \(V_2\)) can travel on the upper arc \(A \rightarrow V_1 \rightarrow B\) or lower arc \(A \rightarrow V_2 \rightarrow B\). The specific setup of this variant of the Braess paradox is taken from here.

Both arcs combine a short bridge and a motorway. The traffic time on the motorways is independent of the amount of cars and it “fixed” at 15 minutes. In contrast, on the bridges the travel time increases with drivers and is defined as (flow / 100) minutes. Naturally, one finds an user equilibrium where both arcs have the same flow. E.g, if the total demand consists of 1000 drivers travelling from A to B, all edges have a flow of 500.

1. User equilibrium

This is easily computed by hand or with the paminco package:

import paminco
import numpy as np

edge_data = np.array([["A", "v1"],
                      ["A", "v2"],
                      ["v1", "B"],
                      ["v2", "B"],
                      ])
marginal_cost = np.array([
  [0, 1/100],  # Bridge A     -> flow/100 minutes
  [15, 0],     # Route R      -> 15 minutes
  [15, 0],     # Route L      -> 15 minutes
  [0, 1/100],  # Bridge B     -> flow/100 minutes
])
demand_data = ("A", "B", 1000)

braess = paminco.Network(
  edge_data=edge_data, 
  cost_data=marginal_cost, 
  demand_data=demand_data,
)
braess.integrate_cost()  # user equilibrium

fw = paminco.NetworkFW(braess)
fw.run(print=False, epsilon=1e-6)
fw.x.round(2)

array([500., 500., 500., 500.])

where we find a travel time of 20 minutes for the lower and upper route:

def route1(x):
    return braess.cost.f(x)[[0, 1]].sum()

def route2(x):
    return braess.cost.f(x)[[2, 3]].sum()

print(f"route 1: {route1(fw.x).round(2)} minutes")
print(f"route 2: {route1(fw.x).round(2)} minutes")

route 1: 20.0 minutes
route 2: 20.0 minutes

2. User equilibrium with artificial road

The government may decide that it would be helpful to add another road, which connects vertices \(V_1\) and \(V_2\) and only takes 7.5 minutes to pass:

edge_data = np.array([["A", "v1"],
                      ["A", "v2"],
                      ["v1", "B"],
                      ["v2", "B"],
                      ["v1", "v2"],
                      ])
marginal_cost = np.array([
  [0, 1/100],  # Bridge A     -> flow/100 minutes
  [15, 0],     # Route R      -> 15 minutes
  [15, 0],     # Route L      -> 15 minutes
  [0, 1/100],  # Bridge B     -> flow/100 minutes
  [7.5, 0]     # Super Road   -> 7.5 minutes
])
demand_data = ("A", "B", 1000)

braess_artificial = paminco.Network(
  edge_data=edge_data, 
  cost_data=marginal_cost, 
  demand_data=demand_data,
)
braess_artificial.integrate_cost()

fw2 = paminco.NetworkFW(braess_artificial)
fw2.run(print=False, epsilon=1e-6)
fw2.x.round(2)

array([750., 250., 250., 750., 500.])

Half of the drivers (500) use this new super road and the government is happy about its efforts. However, all participants now take 22.5 minutes to get from \(A\) to \(B\). The road to hell…

def route1(x):
    return braess_artificial.cost.f(x)[[0, 1]].sum()

def route2(x):
    return braess_artificial.cost.f(x)[[2, 3]].sum()

def route3(x):
    return braess_artificial.cost.f(x)[[0, 4, 3]].sum()

print(f"route 1: {route1(fw2.x).round(2)} minutes")
print(f"route 2: {route2(fw2.x).round(2)} minutes")
print(f"route 3: {route3(fw2.x).round(2)} minutes")

route 1: 22.5 minutes
route 2: 22.5 minutes
route 3: 22.5 minutes