Traffic Networks¶
The modelling of traffic networks is of profound importance in view of reducing carbon emmissions. However, It is no trivial task to model complex networks with a large number selfish of selfish participants. One approach is to caclulate a game theoretical equilibrium, i.e., a state in the game where no participant can improve his/her position by unilateral action [NM44]. In the case of traffic networks this means that all routes a driver might use, take the same amount of time [War52]. This is also called user equilbrium or Wardrop’s first principle developed by John Glen Wardrop.
The computation of the user equilibrium can be reduced to the computation of a minimum cost flow [BMW56]. Thus, paminco can be used to find functions that map a demand multiplier \(\lambda\) to user equilibria \(x_{UE}\). The GitHub repository for transportation research [Tra21] provides data for over 20 traffic networks. This includes toy examples such as the Braess network or SiouxFalls which is used in many publications.
In this user guide you find examples how to calculate (parametric) equilibria – user equilbrium and system optimum – with paminco:
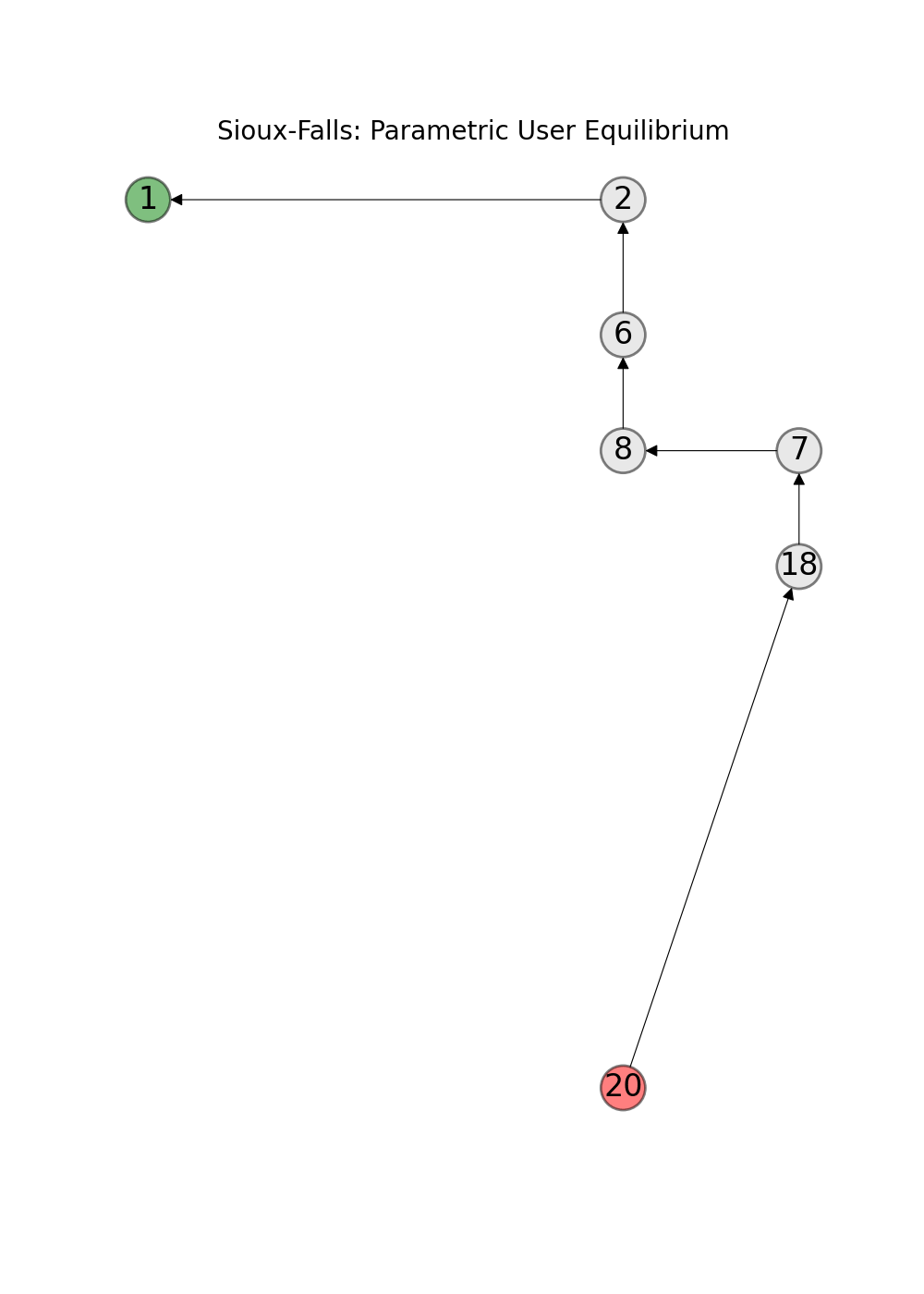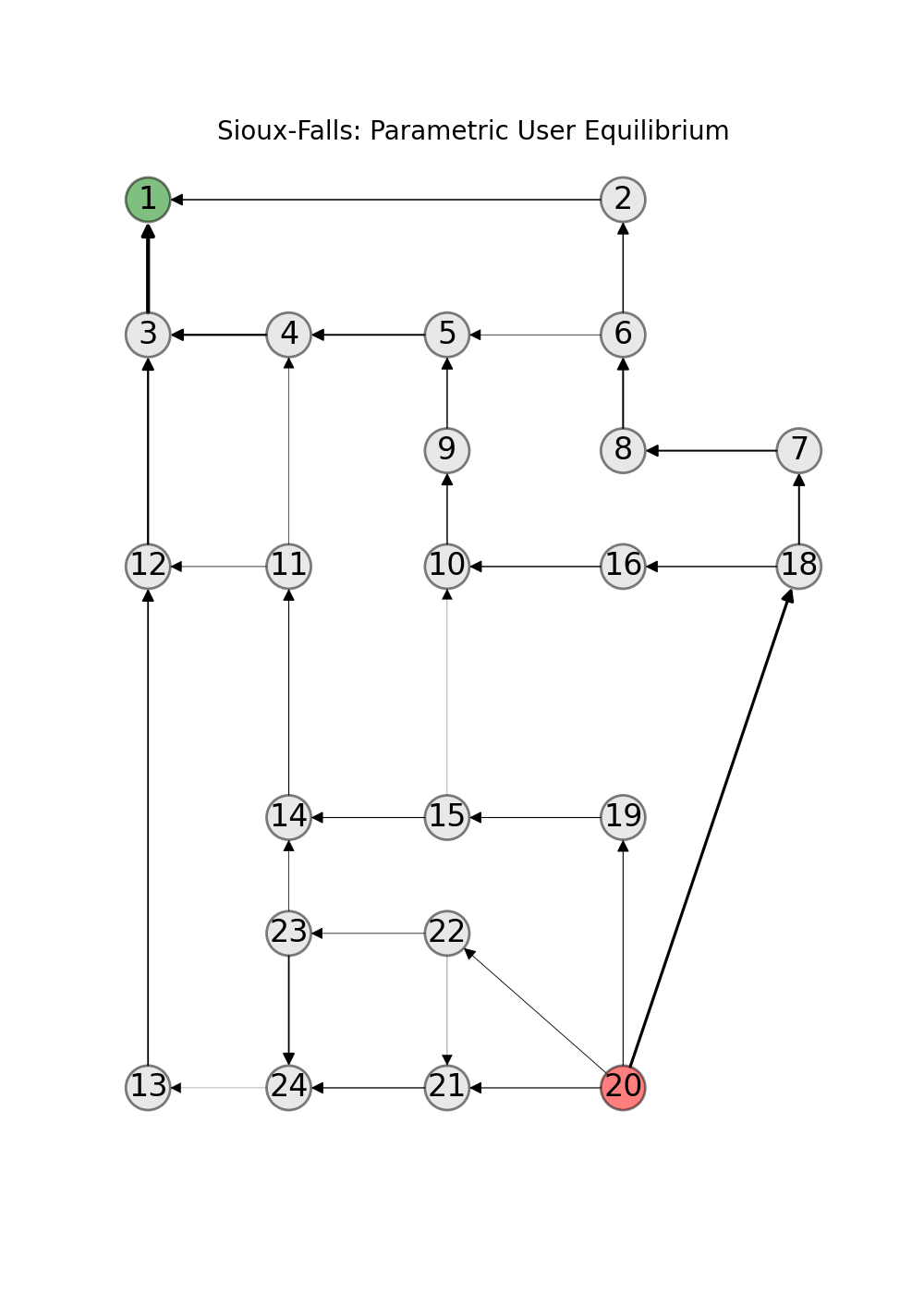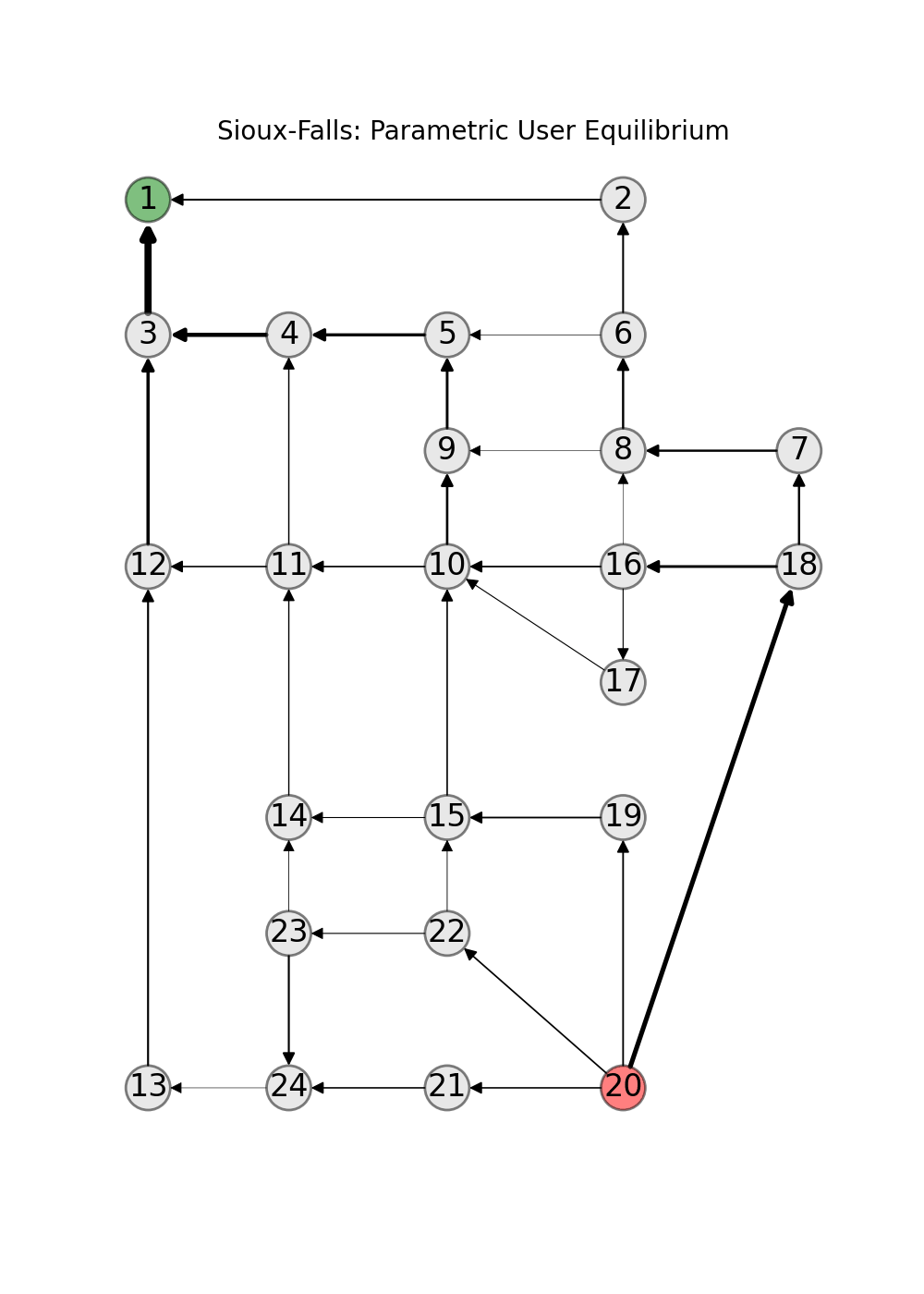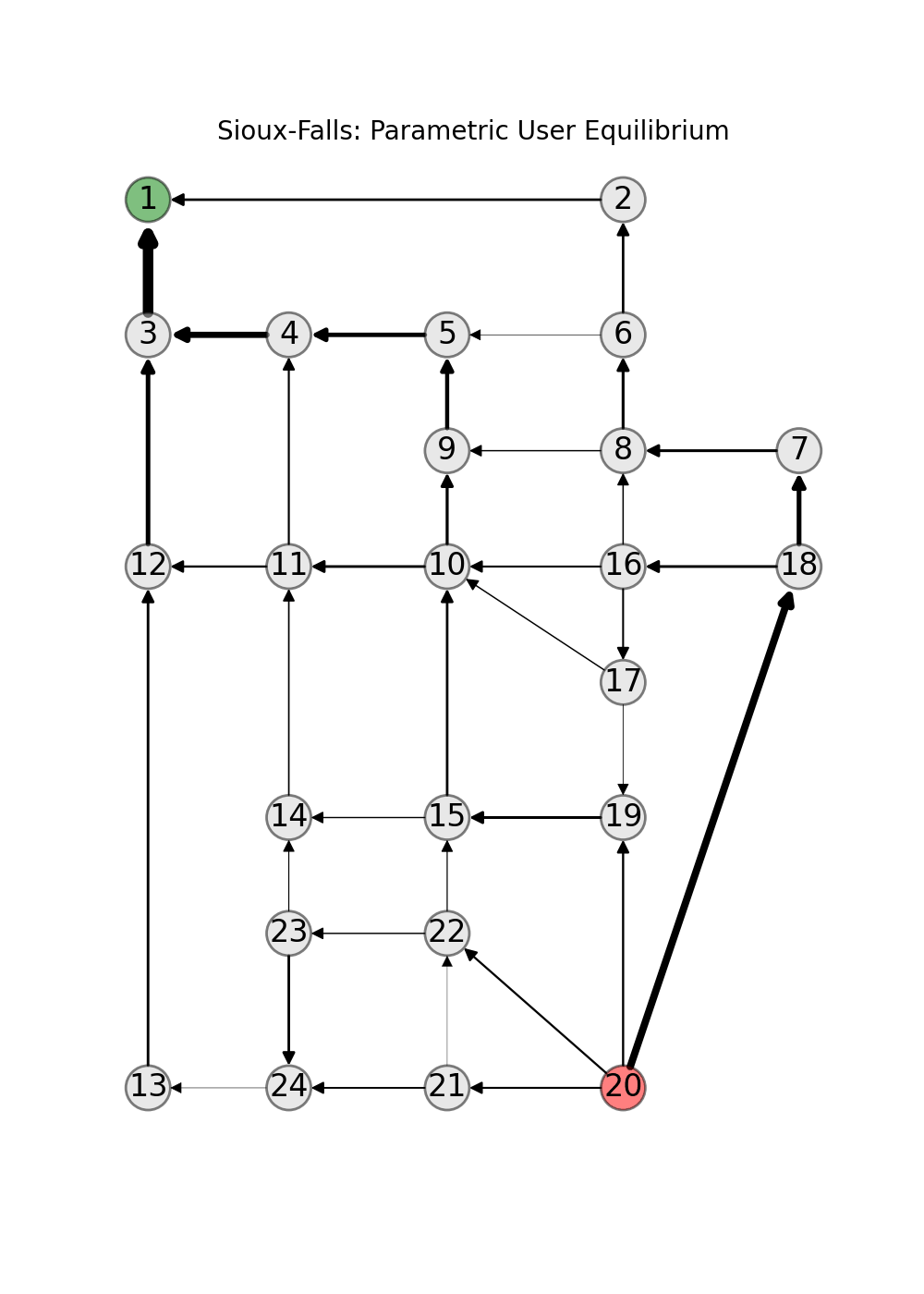
References
- BMW56
Beckmann MJ, McGuire CB, Winsten CB (1956) Studies in the Economics of Transportation. Yale University Press, New Haven, CT.
- NM44
Von Neumann J, Morgenstern O (1944). Theory of Games and Economic Behaviour. Princeton University Press, Princeton.
- Tra21
Transportation Networks for Research Core Team. Transportation Networks for Research. Available at https://github.com/bstabler/TransportationNetworks. Accessed 11, 18, 2021.
- War52
Wardrop JG (1952). “Some theoretical aspects of road traffic research.” In: Proc. Inst. Civil Engrg. 1.3, pp. 325–378.